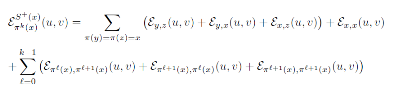
Cover Image

CAPACITARY ESTIMATE ON THE SPACE OF ENDS OF TREE BASED ON ORLICZ NORM

Ryutaro Iijima, Hiroshi Kaneko

DOI Number
10.2298/FUPCT1603243I
First page
243
Last page
255

Abstract


In this article, we will focus on a significance of Ben Amor’s result which reveals an important relationship between Orlicz norm and a capacitary estimate. We will derive a lower capacitary estimates from spectral analytic overviews based on the scheme and recent development of stochastic analytic schemes on the ends of a tree. In particular, as an application of our analytical approach, we will shed light on a capacitary estimate for singleton given as an end of the tree.


Keywords

capacitary estimate, tree, Orlicz norm

Full Text:

PDF

References


S. Albeverio and W. Karwowski: A random walk on p-adics - the generator and its spectrum. Stochastic Proc. Appl. 53 (1994) 1-22.

S. Albeverio and W. Karwowski: Jump processes on leaves of multibranching trees. J. Math. Phys. 49 (2008) 093503, 20pp.

M. Baxter: Markov processes on the boundary of the binary tree. Lecture Notes in Math. SLeminaire de ProbabilitLes, XXVI, Lecture Notes in Math., Volume 1526. 210–244. Springer, Berlin, 1992.

Z. Q. Chen and M. Fukushima: Symmetric Markov processes, time changes, and boundary theory. Princeton Univesirty Press, Princeton, 2012.

J. L. Doob: Boundary properties for functions with finite Dirichlet integrals. Ann. Inst. Fourier (Grenoble) 12 (1962) 573–621.

M. Fukushima, Y. Oshima, and M. Takeda: Dirichlet forms and symmetric Markov processes. Walter de Gruyter (1994).

C. Hara, R. Iijima, H. Kaneko, H. Matsumoto: Orlicz norm and Sobolev-Orlicz capacity on ends of tree based on probabilistic Bessel kernels. p-Adic Numbers, Ultrametric Analysis, and Applications 7 (2015) 24–38

M. Fukushima, H. Kaneko: On (r, p)-capacities for general Markovian semi-groups. in S. Albeverio (ed.), Stochastic Process and Infinite Dimensional Analysis, Pitman, 1983.

H. Kaneko: A class of spatially inhomogeneous Dirichlet spaces on the p-adic number field. Stochastic Proc. Appl. 88 (2000) 161–174.

H. Kaneko, K. Yasuda: Capacities associated with Dirichlet space on an infinite extension of a local field. Forum Math. 17 (2006) 1011–1032.

H. Kaneko: (r, p)-capacity and Hausdorff measure on a local field. Indag. Math. 17 (2006) 251–270.

H. Kaneko: A Dirichlet space on ends of tree and Dirichlet forms with a nodewise orthogonal property. Potential Analysis 41 (2014) 245–268.

H. Kaneko: A Dirichlet space on ends of tree and superposition of nodewise given Dirichlet forms with tier linkage. in (ed.) N.Jacob, M. Takeda, T. Uemura, Festschrift Masatoshi Fukushima: In Honor Of Masatoshi Fukushima’s Sanju Potential Analysis, World Scientific, 237–262, 2014.

J. Kigami: Dirichlet forms and associated heat kernels on the Cantor set induced by random walks on trees. Adv. in Math. 225 (2010) 2674–2730

J. Kigami: Transitions on a noncompact Cantor set and random walks on its defining tree. Ann. Inst. H. Poincare Probab. Statist., 49 (4), (2013) 1090–1129.

A. Ben Amor: Sobolev-Orlicz inequalities, ultracontractivity and spectra of time changed Dirichlet forms.Math. Z. 255 (2007) 627–647.

Rao, M. M., Ren, Z. D: Theory of Orlicz spaces. Pure and Applied Math. 146 Marcel Dekker Inc., New York, 1991.

V. S. Vladimirov, I. V. Volovich and E. I. Zelenov: P-Adic Analysis and Mathematical Physics. Series on Soviet and East European Mathematics, World Scientific, Singapore, New Jersey, London, Hong Kong (1995).


Refbacks

  • There are currently no refbacks.


ISSN 0354-4656 (print)

ISSN 2406-0879 (online)